Перечитав множество сайтов по этой задаче, везде предлагают решать ее
жадным алгоритмом,
но после всех поисков я так и не понял: "как в жадном алгоритме находится следующая точка?"
В
статье википедии нет четкого определения человеческим языком.
Часто вообще сразу дают примеры, а ты по формулам должен прочитать и понять(
пример).
vovafed писал(а):в арткаме можно надо разбить на зоны.
зоны сгрупировать в нужной последовательности и считать программу.
но трудоемко получается надо векторами обрисовать так чтобы минимизировать нагрузку на фрезу
т.е. в арткаме нужно вручную задавать последовательность обхода зон?
Nick писал(а):Во сколько ты оценишь реальное максимальное количество островков?
michael-yurov писал(а):Сколько переходов обычно бывает при создании траектории? 10? 100? 1000? 10 000?
у каждого по разному. У меня выходит около сотни.
michael-yurov писал(а):Я перепутал с задачей поиска кратчайшего маршрута.
вообще-то "задача комивояжера" это и есть "задача комивояжера по нахождению катчайшего маршрута". Нет?
michael-yurov писал(а):Даже для 10 000 переходов можно легко перебрать все варианты, это займет доли секунды.
michael-yurov писал(а):А можно не искать лучший маршрут, а лишь перебрать несколько тысяч / миллионов и выбрать из них наиболее удачные.
В
этой статье под названием "Задача комивояжера" говорится:
Метод полного перебора (иногда говорят Метод перебора, подразумевая при этом полный перебор - это не совсем правильно, так как перебор может быть и не полным) заключается в том, что выполняется перебор всех возможных комбинаций точек (пунктов назначения). Как известно из математики, число таких перестановок равно n!, где n – количество точек. Так как в задаче коммивояжера исходный пункт обычно принимается одним и тем же (первая точка), то нам достаточно перебрать оставшиеся, т.е. количество перестановок будет равно (n–1)!. Этот алгоритм почти всегда дает точное решение задачи коммивояжера, однако продолжительность таких вычислений может занять непозволительно много времени. Известно, что при значениях n > 12, современный(?) компьютер не смог бы решить задачу коммивояжера даже за все время существования вселенной.
Нашел "красивое" решение задаче о сверлильном станке на сайте rusnauka.com.
Во первых автор Петричкович Александр Анатольевич сам придумал этот алгоритм,
который как оказалось позже - уже существовал под названием "Волновой алгоритм (Алгоритм Ли)",
что говорит о том, что из всех вариантов решений он один из наиболее оптимальных.
во 2х - он решал
как раз нашу задачу о сверлильном станке и оптимизации пути.
в 3-х - он пробовал решать нашу задачу и жадным алгоритмом и волновым, но остановился на волновом.
в 4-х он не теоретик, а практически еще и написал программу на дэлфях,
да и сам алгоритм достаточно прост как в реализации так и в понимании принципа работы.
Буду делать волновым алгоритмом.
Описание:
Волновой алгоритм является одним из самых уникальных алгоритмов трассировки. Он позволяет построить трассу (путь) между двумя элементами в любом лабиринте.
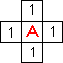
- волновой алгоритм, первая волна.gif (447 байт) 2087 просмотров
Из начального элемента распространяется в 4-х(?) направлениях волна. Элемент, в который пришла волна образует фронт волны. На рисунках цифрами обозначены номера фронтов волны.
Каждый элемент первого фронта волны является источником вторичной волны.
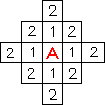
- волновой алгоритм, вторая волна.gif (811 байт) 2087 просмотров
Элементы второго фронта волны генерируют волну третьего фронта и т.д. Процесс продолжается до тех пор, пока не будет достигнут конечный элемент.
Перефразируя: берем текущую позицию станка(точку) в качестве текущей волны(массив точек №1).
Проверяем есть ли в текущей волне(массиве точек) соседняя точка.
Если есть - эта точка ближайшая - берем ее и останавливаемся и переходим в неё, иначе продолжаем.
Вокруг(?еще не придумал как реализовать

?) текущей волны запоминаются все соседние точки в качестве следующей волны(массив точек №2).
Текущей волной становится волная №2, волну №1 - забываем.
Возвращаемся в начало цикла.

